[백준] 4963 - 섬의 개수 (C++)

https://www.acmicpc.net/problem/4963

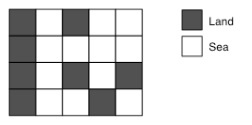
정사각형으로 이루어져 있는 섬과 바다 지도가 주어진다. 한 정사각형과 가로, 세로 또는 대각선으로 연결된 사각형은 걸어갈 수 있는 사각형이다. 한 정사각형에서 다른 정사각형으로 걸어서 갈 수 있는 경로가 있을 경우 두 정사각형을 하나의 섬으로 본다. 지도는 바다로 둘러싸여 있으며, 지도 밖으로 나갈 수 없다. 최종적으로 지도가 주어질 때 섬의 개수를 세는 문제다.

 

---

문제 탐색하기

- 문제에서 구해야 하는 최종 정답은 무엇인지 탐색한 과정
- 그 정답을 구하기 위해 어떻게 코드를 구현해야 할지 고민한 과정
- 문제에 들어오는 범위를 파악하며 어떤 알고리즘을 쓸 수 있을지 고민해 가는 과정

ex. 가능한 시간 복잡도, 알고리즘 선택

입출력 제한

• 1 ≤ w, h ≤ 50

 

2차원 배열이 주어지고 해당 배열의 한 점에서 이어진 다른 점들을 찾는 문제는 주로 너비 우선 탐색이나 깊이 우선 탐색을 이용해서 푼다. 나는 깊이 우선 탐색보단 너비 우선 탐색을 주로 이용해서 구현한다. 배열과 배열의 방문 정보를 기록할 배열을 따로 선언하고 이 정보들을 이용해 이어진 점들을 모두 찾을 수 있다.

• 너비 우선 탐색은 queue를 이용하며, 해당 점에 연결된 주변 점들을 모두 queue에 넣으면서 진행한다. queue에 넣은 적이 있는 점은 다시 방문할 필요가 없으므로 방문 여부를 저장할 배열도 필요하다. 이때 가로, 세로, 대각선까지 8방향을 모두 확인해야 한다.
• 깊이 우선 탐색은 stack이나 재귀 함수를 이용한다. stack을 이용하는 경우, 위와 비슷하게 해당 점에 연결된 주변 점들을 모두 stack에 넣으면서 진행한다. 재귀 함수를 이용한다면 stack에 넣을 필요 없이 방문 표시만 제대로 하면 된다.
• queue나 stack을 이용한다면 자료구조에 원소를 넣으면서 방문 표시를 하고, 재귀 함수를 이용한다면 함수 가장 위에서 방문 표시를 해야 한다.

// 재귀 함수를 이용한 깊이 우선 탐색
void dfs(int x, int y) {
  visit[x][y] = 1;
  for (int i=0; i<8; i++) {
    int cx = x+dx[i], cy = y+dy[i];
    if (cx<0 || cy<0 || cx>=n || cy>=m || visit[cx][cy] || !board[cx][cy]) continue;
    dfs(cx,cy);
  }
}

// stack을 이용한 깊이 우선 탐색 -> 정답 코드에서 stack으로 바꿔서 조금만 바꾸면 됨

 

지도와 방문 정보를 전역 변수로 선언했기 때문에 테스트 케이스가 초기화될 때마다 지도와 방문 정보도 같이 초기화해야 한다는 걸 고려해야 한다. 섬의 개수를 나타내는 변수는 테스트 케이스마다 선언하도록 하면 된다. 추가로 너비가 w고 높이가 h라 구현하면서 헷갈릴 수 있어서 h와 w 순서로 입력받는 게 낫다.

 

---

코드 설계하기

위의 [문제 탐색하기]에서 고민한 과정을 토대로 문제 풀이에 대한 실마리를 잡고, 문제 풀이를 본격적으로 하기 전 이 문제를 풀기 위한 로드맵을 그리는 과정!

- 어떤 순서로 코드를 작성해야 할지
- 어떤 함수들을 작성해야 할지

1. w, h 입력받기
   1. w와 h가 모두 0이라면 입력 종료
2. 지도 정보 입력받기
3. 이중 반복문을 통해 방문한 적 없는 땅에 도착하면 너비 우선 탐색 함수로 걸어서 갈 수 있는 모든 땅에 방문 표시하기
   1. 너비 우선 탐색 함수를 돌린 횟수 = 섬의 개수
   2. queue에 방문한 위치를 넣으면서 함수 진행하기 (현재 위치에서 8방향 모두 탐색)
4. 섬의 개수 출력하기

 

---

시도 회차 수정 사항 (Optional)

- '틀렸습니다'를 받았다면 왜 틀렸는지 고민해보고, 어떻게 수정할 수 있는지 고민하는 과정을 작성
- 내가 세울 설계에서 어떤 부분이 틀렸는지도 함께 점검
- 한 번에 맞히면 pass해도 됨!

pass

 

---

정답 코드

#include <iostream>
#include <queue>
#define pii pair<int,int>
using namespace std;

int w,h,dx[8]={0,0,-1,-1,-1,1,1,1},dy[8]={-1,1,-1,0,1,-1,0,1};
bool board[50][50],visit[50][50];

void bfs(int x, int y) {
    queue<pii> q;
    q.push({x,y});
    visit[x][y] = true;
    while (!q.empty()) {
        auto [a,b] = q.front();
        q.pop();
        for (int i=0; i<8; i++) {
            int cx=a+dx[i],cy=b+dy[i];
            if (cx<0 || cy<0 || cx>=w || cy>=h || visit[cx][cy] || !board[cx][cy]) continue;
            q.push({cx,cy});
            visit[cx][cy] = true;
        }
    }
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    while (1) {
        cin >> h >> w;
        if (w==0 && h==0) break;
        fill(&board[0][0],&board[50][0],0);
        for (int i=0; i<w; i++)
            for (int j=0; j<h; j++) cin >> board[i][j];
        
        fill(&visit[0][0],&visit[50][0],0);
        int ans = 0;
        for (int i=0; i<w; i++) {
            for (int j=0; j<h; j++) {
                if (board[i][j] && !visit[i][j]) {
                    bfs(i,j);
                    ans++;
                }
            }
        }
        
        cout << ans << '\n';
    }
}